Matrix

Motivation

On a traditional supervised machine learning problem using structured and tabular data, often we have to create a model based on a previous dataset. The model must learn and then map the independent variables (features) $x$ into a dependent variable (target) $y$. This problem can be represented as a system of linear equations as shown below:

$$\{\begin{array}{l}{w}_1{x}_1^{(1)}+w_2{x}_2^{(1)}+w_3{x}_3^{(1)}+...+w_n{x}_n^{(1)}+b=y^{(1)}\\ w_1{x}_1^{(2)}+w_2{x}_2^{(2)}+w_3{x}_3^{(2)}+...+w_n{x}_n^{(2)}+b=y^{(2)}\\ w_1{x}_1^{(3)}+w_2{x}_2^{(3)}+w_3{x}_3^{(3)}+...+w_n{x}_n^{(3)}+b=y^{(3)}\\ ⋮\\ w_1{x}_1^{(m)}+w_2{x}_2^{(m)}+w_3{x}_3^{(m)}+...+w_n{x}_n^{(m)}+b=y^{(m)}\end{array}$$

Solve the system of linear equations for $[w_1,w_2,w_3,...,w_n,b]$.

$$\left[\begin{array}{ccccc}{w}_1& w_2& w_3& ...& w_n\end{array}\right]\left[\begin{array}{ccccc}{x}_1^{(1)}& x_2^{(1)}& x_3^{(1)}& ...& x_n^{(1)}\\ x_1^{(2)}& x_2^{(2)}& x_3^{(2)}& ...& x_n^{(2)}\\ x_1^{(3)}& x_2^{(3)}& x_3^{(3)}& ...& x_n^{(3)}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ x_1^{(m)}& x_2^{(m)}& x_3^{(m)}& ...& x_n^{(m)}\end{array}\right]\left[\begin{array}{ccccc}{y}^{(1)}& y^{(2)}& y^{(3)}& ...& y^{(n)}\end{array}\right]$$ $$\vec{w}\cdot X+b=\vec{\hat{y}}$$

System Types

• $(I)$ Complete - Non-Singular (Unique Solution)
• $(II)$ Redundant - Singular (Infinite Solutions)
• $(III)$ Contradictory - Singular (No Solution)

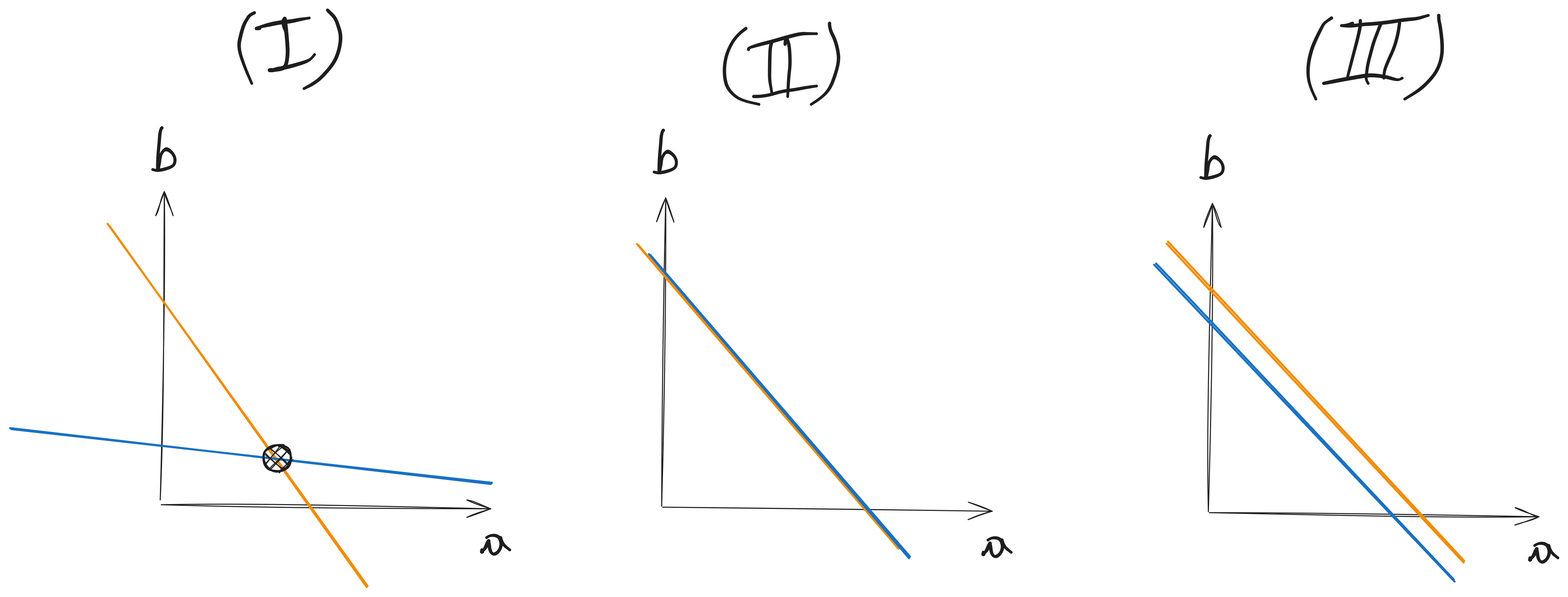
Linear Dependence and Independence

$$\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 2\\ 1& 1& 3\end{array}\right]\to (R1+R3)÷2=R2\to [112](LinearDependent)$$

Determinant

If the $Det(A)\ne 0$, then the matrix $A$ is non-singular. Also, the determinant can be interpreted geometrically as the area or volume of a linear transformation basis.

$$A=\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 10\end{array}\right]$$ $$\begin{gathered} Det(A)=(1\cdot 5\cdot 10+2\cdot 6\cdot 7+3\cdot 4\cdot 8) \\ - \\ (3\cdot 5\cdot 7+6\cdot 8\cdot 1+10\cdot 4\cdot 2)=-3 \end{gathered}$$

Determinant of a Product

$$det(\mathbf{AB})=det(\mathbf{A})\cdot det(\mathbf{B})$$

Determinant of Inverse

$$det({\mathbf{A}}^{-1})=\frac{1}{det(\mathbf{A})}$$

Determinant of Identity

$$det(\mathbf{I})=1$$

Elementary Row Operations (EROs)

• Switch rows
• Multiply row by a (non-zero) scalar
• Add a row to another row

Row Echelon Form (REF)

• Zero rows are at the bottom
• Each row has a pivot (leftmost non-zero entry)
• Every pivot is to the right of the pivots on the rows above
• Rank of the matrix is the number of pivots

$$\left[\begin{array}{ccccc}\text{3}& \ast & \ast & \ast & \ast \\ 0& 0& \text{1}& \ast & \ast \\ 0& 0& 0& \text{-4}& \ast \\ 0& 0& 0& \text{0}& 0\\ 0& 0& 0& 0& \text{0}\end{array}\right]$$

Reduced Row Echelon Form (RREF)

• The matrix must be in row echelon form
• Each pivot is a $1$
• Any number above the pivot has to be $0$
• Rank of the matrix is the number of pivots

$$\left[\begin{array}{ccccc}\text{1}& \ast & 0& 0& \ast \\ 0& 0& \text{1}& 0& \ast \\ 0& 0& 0& \text{1}& \ast \\ 0& 0& 0& \text{0}& 0\\ 0& 0& 0& 0& \text{0}\end{array}\right]$$

Rank

The rank of a matrix can be seen as a measure of the information amount present on a system. It can be interpreted as the number of linear independent equations that make up a system.

If a matrix $A$ have a full rank, it means the rank is equal to the matrix order ($Rank(A)=n$ for $A_{n\times n}$), then the system is non-singular.

The rank of a matrix can be calculated based on the number of pivots in the row echelon form.

$$M=\left[\begin{array}{ccc}\text{1}& 2& 3\\ 0& \text{1}& 7\\ 0& 0& \text{1}\end{array}\right]$$

$Rank(M)=3$

Gaussian Elimination Algorithm

Is a method for row reduction and so for solving linear systems.

1. Create the augmented matrix
2. Get the matrix into reduced row echelon form
3. Complete back substitution
4. Stop if you encounter a row of zeros (singular system)

Augmented Matrix

$$\{\begin{array}{l}2a-b+c=1\\ 2a+2b+4c=-2\\ 4a+b=-1\end{array}$$ $$\left[\begin{array}{cccc}2& -1& 1& 1\\ 2& 2& 4& -2\\ 4& 1& 0& -1\end{array}\right]$$

Matrix Inverse

Analogous to a number multiplicative inverse, a square $m\times m$ matrix $\mathbf{A}$ is invertible (also non-singular) if there exists an $m\times m$ square matrix ${\mathbf{A}}^{-1}$ such that:

$$\mathbf{A}{\mathbf{A}}^{-1}={\mathbf{A}}^{-1}\mathbf{A}={\mathbf{I}}_m$$

where ${\mathbf{I}}_m$ denotes the $m\times m$ identity matrix.

• A matrix is invertible only if $Det(\mathbf{A})\ne 0$.

Identity Matrix

The identity matrix of size $m$ is the $m\times m$ square matrix with ones on the main diagonal and zeros elsewhere. Analogous to multiplying a number by $1$, the multiplied object remains the same.

$$\mathbf{IA}=\mathbf{AI}=\mathbf{A}$$