Linear Transformation (LT)

Matrices as Linear Transformation (LT)

Matrices can be used to map a vector from a space to another one, acting like a factor for changing coordinates (LT).

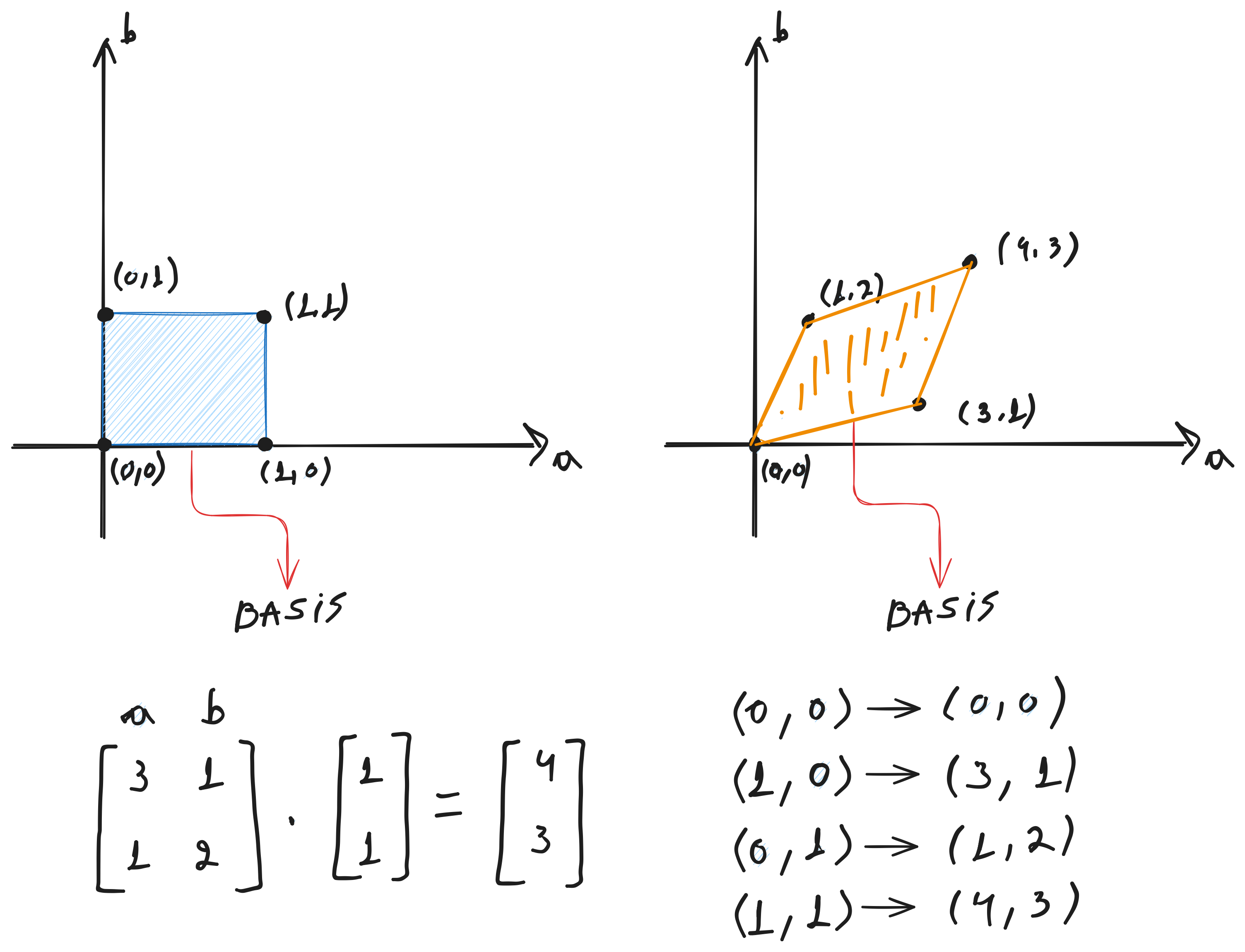
Also, given some mapped vectors is possible to obtain the matrix $\mathbf{M}$ responsible by the linear transformation:

$$\mathbf{M}=\left[\begin{array}{cc}?& ?\\ ?& ?\end{array}\right]$$ $$\mathbf{M}\cdot \left[\begin{array}{c}0\\ 1\end{array}\right]=\left[\begin{array}{c}2\\ 3\end{array}\right]$$ $$\mathbf{M}\cdot \left[\begin{array}{c}1\\ 0\end{array}\right]=\left[\begin{array}{c}3\\ -1\end{array}\right]$$ $$\mathbf{M}=\left[\begin{array}{cc}3& 2\\ -1& 3\end{array}\right]$$

Matrix vs Matrix Multiplication

The multiplication of one matrix by another one can be interpreted as a combined two consecutive linear transformations. In the expression below the linear transformation $\mathbf{A}$ occurs after the first LT $\mathbf{B}$.

$${\mathbf{A}}_{2\times 3}\cdot {\mathbf{B}}_{3\times 4}={\mathbf{C}}_{2\times 4}$$

Singularity and Rank of LT

• The singular LT basis only covers a small piece of the plane (line or a point).
• The dimension of the basis is equal to the LT rank.
• The determinant can be seen as the area or volume of the LT basis.

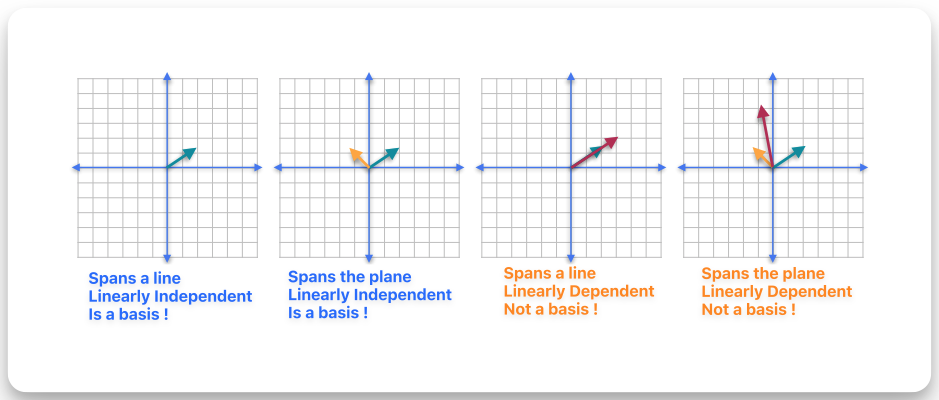
Bases

A basis is a vector set that satisfies the two conditions:

• They are linear independently
• The set spans a vector space

Attention

Not all sets of $N$ vectors are a basis for $N$-dimensional space.